1010번: 다리 놓기
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
www.acmicpc.net
풀이
DP를 사용하여 해결했습니다.
예를들어 N = 2, M = 5이고
i = 1, j = 1이라면
왼쪽에 한개, 오른쪽에 한개의 사이트이므로

위 이미지와 같이 1개의 연결이 가능합니다.
i = 1, j = 5라면
왼쪽에 1개 오른쪽에 5개의 사이트가 있으므로
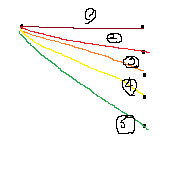
위 이미지와 같이 5가지 경우로 연결이 가능합니다.
이를 그래프로 표현하면
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 1 | 2 | 3 | 4 | 5 |
가 됩니다.
다음으로 i = 2이고 j = 1일 경우에는

위 그림과 같이 2개의 다리가 설치되어야하지만 교차가 안되므로 0개의 연결이 가능합니다.
다음으로 i = 2, j = 3일 경우에는

위 이미지와 같이 3가지의 경우가 있다는것을 볼 수 있습니다.
이러한 점을 이용해서
i = 2, j = 5까지의 그래프를 만들어보면
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 0 | 1 | 3 | 5 | 10 |
가 됩니다.
이를 쉽게 구하는 방법은
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 1 | 2 | 3 | 4 | 5 |
| 2 | 0 | 1 | 3 | 5 | 10 |
i = 2이고 j = 3인 경우의 수는 3인데 이는 i = 1일때의 j = 3 이전의 경우의 수들의 합이므로
이를 이용하여 그래프를 쉽게 만들 수 있습니다.
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
public static long[][] memo;
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
for (int tc = 0; tc < T; ++tc) {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
memo = new long[31][31];
// 하나의 다리를 두는 경우를 구한다.
for (int i = 1; i <= M; ++i) {
// 이때 i개의 동쪽 사이트에 하나의 다리를 두는 경우의 수는 i개가 된다.
memo[1][i] = i;
}
// 2개이상의 다리를 놓는 경우의 수를 구한다.
for (int i = 2; i <= N; ++i) {
// 다리는 겹치면 안되므로 i 아래로만 새로운 다리를 놓을 수 있다!
// i는 다리의 개수이므로 만약 두개의 다리를 놓는다면
// 왼쪽 2번 사이트가 오른쪽 1번 사이트로 연결할 경우
// 다리가 교차되어 최대의 다리개수가 안되므로 i번 이후의 다리들만 보면 된다.
// memo에는 이전 i - N개의 다리를 연결하는 가지수들이 저장되어있기 때문에 가능
for (int j = i; j <= M; ++j) {
// i 아래에 세워지는 다리는 절! 대! i를 넘을 수 없다는 것에 주의
// 마찬가지로 오른쪽 사이트 번호까지 i개의 다리를 설치할 수 있는 경우를 볼때에도
// i는 다리의 개수이므로 다리끼리 교차되면 안되므로 i번 이후의 다리들만 보면된다.
for (int k = j - 1; k >= 0; k--) {
// 만약 2개의 다리를 3번 동쪽 포인트까지만 설치한다면
// 다리는 교차될 수 없고 1번에 다리가 설치되는 경우들을 본 후,
// 2번에 다리가 설치되는 경우들을 보면 3번에 다리를 설치할 수 있는 경우들을 볼 수 있으므로
// i개의 다리를 설치하는 경우의 수는
// i - 1개의 다리를 설치할 때의 j번의 동쪽 포인트이전의 경우의수를 전부 더해주면된다.
memo[i][j] += memo[i - 1][k];
}
}
}
System.out.println(memo[N][M]);
}
}
}
pyo7410/Algorithm
1일 1커밋을 목표로! Contribute to pyo7410/Algorithm development by creating an account on GitHub.
github.com
'알고리즘 > 백준' 카테고리의 다른 글
| [Java] BOJ 11057번 오르막 수 (0) | 2021.04.22 |
|---|---|
| [Java] BOJ 9465번 스티커 (0) | 2021.04.21 |
| [Java] BOJ 11052번 카드 구매하기 (0) | 2021.04.15 |
| [Java] BOJ 14501번 퇴사 (0) | 2021.04.14 |
| [Java] BOJ 11727번 2xn 타일링 2 (0) | 2021.04.09 |